2D 流体
因为最近工作原因,需要处理2D流体相关的一些图形仿真,这篇博客是对工作中学习到的一些2D流体图形的知识等记录,主要参考了知乎博主“光影帽子”的文章、B站上的王洪伟老师的流体力学教学视频,以及GPU Gems,其他参考者恐有遗漏,如有冒犯,敬请见谅、告知。另外,因本人才学疏浅,文章难免有所纰漏,一并敬请告知,感谢🙏
相关概念
扩散 Diffusion
将一滴染料滴在清水中,那么染料会在水中扩散,也就是随机朝四面八方移动。
粘度 Viscosity
根据实际流体的经验,有些流体比其他流体“更稠”。例如,糖蜜和枫糖浆流动缓慢,而外用酒精流动迅速。我们说粘稠的流体具有高粘度。粘度是衡量流体流动阻力大小的指标。这种阻力影响动量(以及速度)的扩散。
平流 Advection
如果清水原本也有速度,那么染料也会随着这个速度移动,这就是平流。
对流 Convection
对流与平流基本上是同义词,唯一区别是,平流是指在水中的其它物质的移动,对流是指流体本身的移动。
压力 Pressure
因为流体的分子可以相互移动,所以它们倾向于相互“挤压”和“晃动”。当对流体施加力时,它不会立即传播到整个体积。相反,靠近力的分子会推向远处的分子,压力就会增加。因为压力是单位面积的力,流体中的任何压力自然会导致加速度(想想牛顿第二定律)。
外力 External Forces
第四项包含由于施加到流体上的外力引起的加速度。这些力可能是局部力或全局力。局部力被施加到流体的特定区域——例如,风扇吹空气的力。全局力,例如重力,均匀地作用于整个流体。
散度 Divergence
假如有一个无限长的大厅,我们将它划分为很多方形区域。每个区域都有一些人,人可能会到处移动。现在我们想知道在某个区域的人,离开这个区域的程度,怎么算呢?比如区域E,原来有一些人,现在单位时间内有u个人从左右边界离开,有 v 个人从上下边界离开,现在区域E少了多少人? 答案很简单,就是 u + v ,我们可以叫它”某个东西离开这个区域的程度”或”分散程度“,或者简称叫做“散度”,英文Divergence。 所以说,散度描述的是一个向量场的发散程度,它是一个标量。
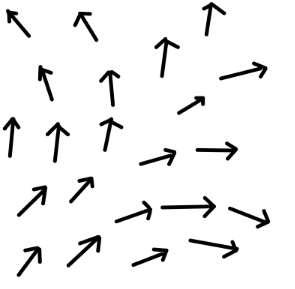
衡量的是在某一点出相应的向量聚集或者发散程度,测量方向为径向,速度的散度如下:
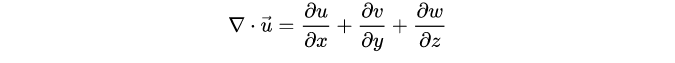
如上图所示,这个速度场明显是发散的,而为什么会发散呢?总得有个来源吧?所以从物理上讲,散度描述的是一个场里的有源性,如果 \(div F > 0\) ,说明场内存在产生通量的正源;如果 \(div F < 0\) ,说明场内存在吞噬通量的负源;如果 \(div F = 0\) ,说明场内没有任何源。
散度定理
这是一个一般的结论,对二维空间来说,如果将一个大区域分成很多小区域,那么
从大区域的边界上的总离开量 = 各个小区域的净离开量相加
三维散度定理,说人话就是,将三维坐标系上的一个三维大空间分成许多三维小空间,那么
从大空间的边界上的总离开量 = 各个小空间的净离开量相加
旋度 Curl
旋度(Curl),顾名思义,它是描述三维向量场对某一点附近的微元造成的旋转程度。 衡量的是某点的旋转速度,测量方向为切向,三维形式的旋度是一个向量,因为使用了外积,如果降到二维形式则是一个标量:
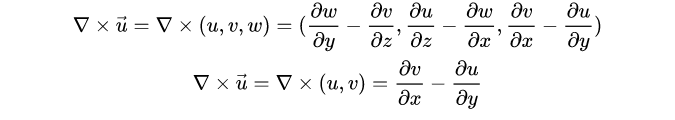
连续性方程

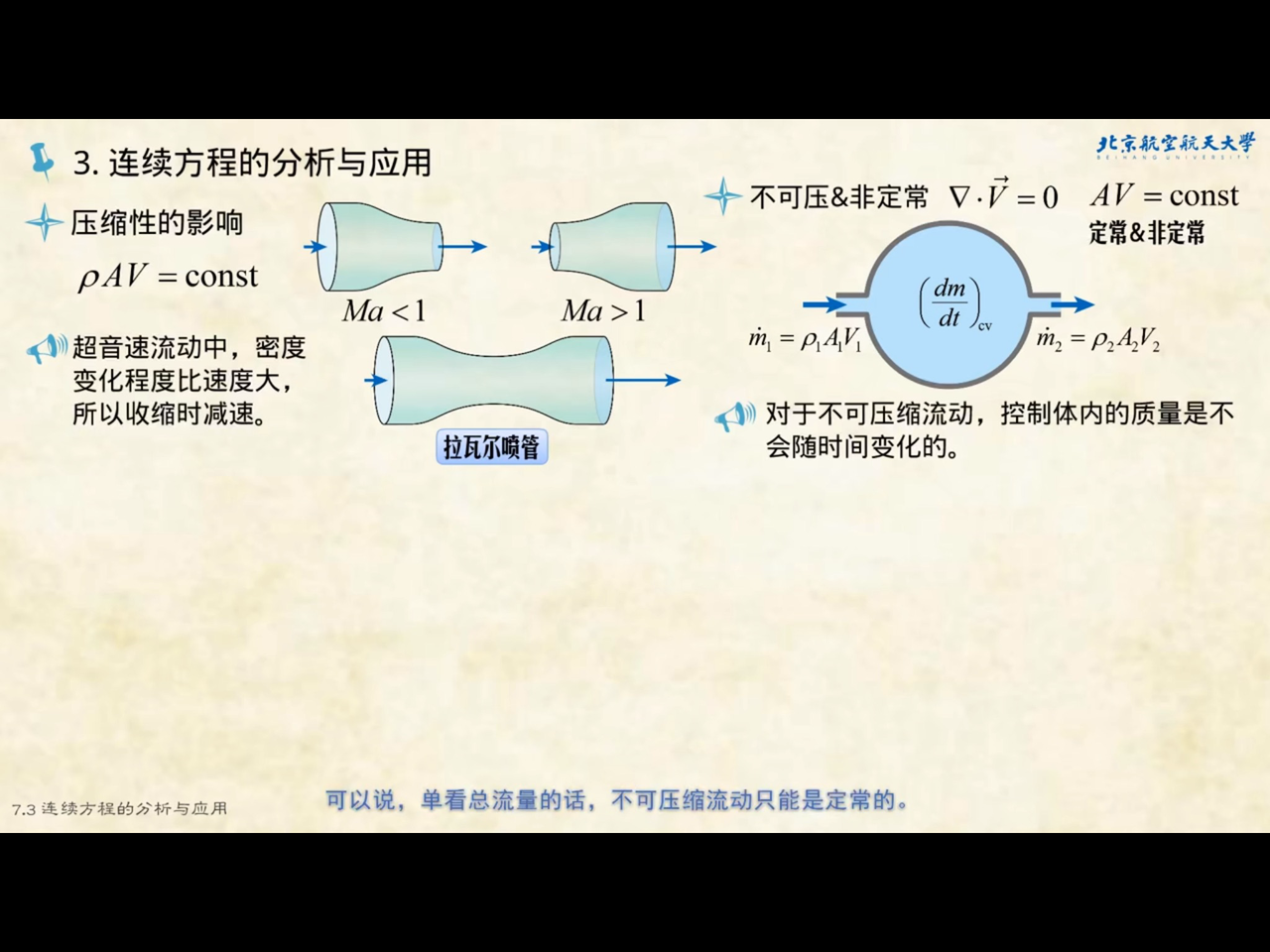
可压缩性

不可压缩流体
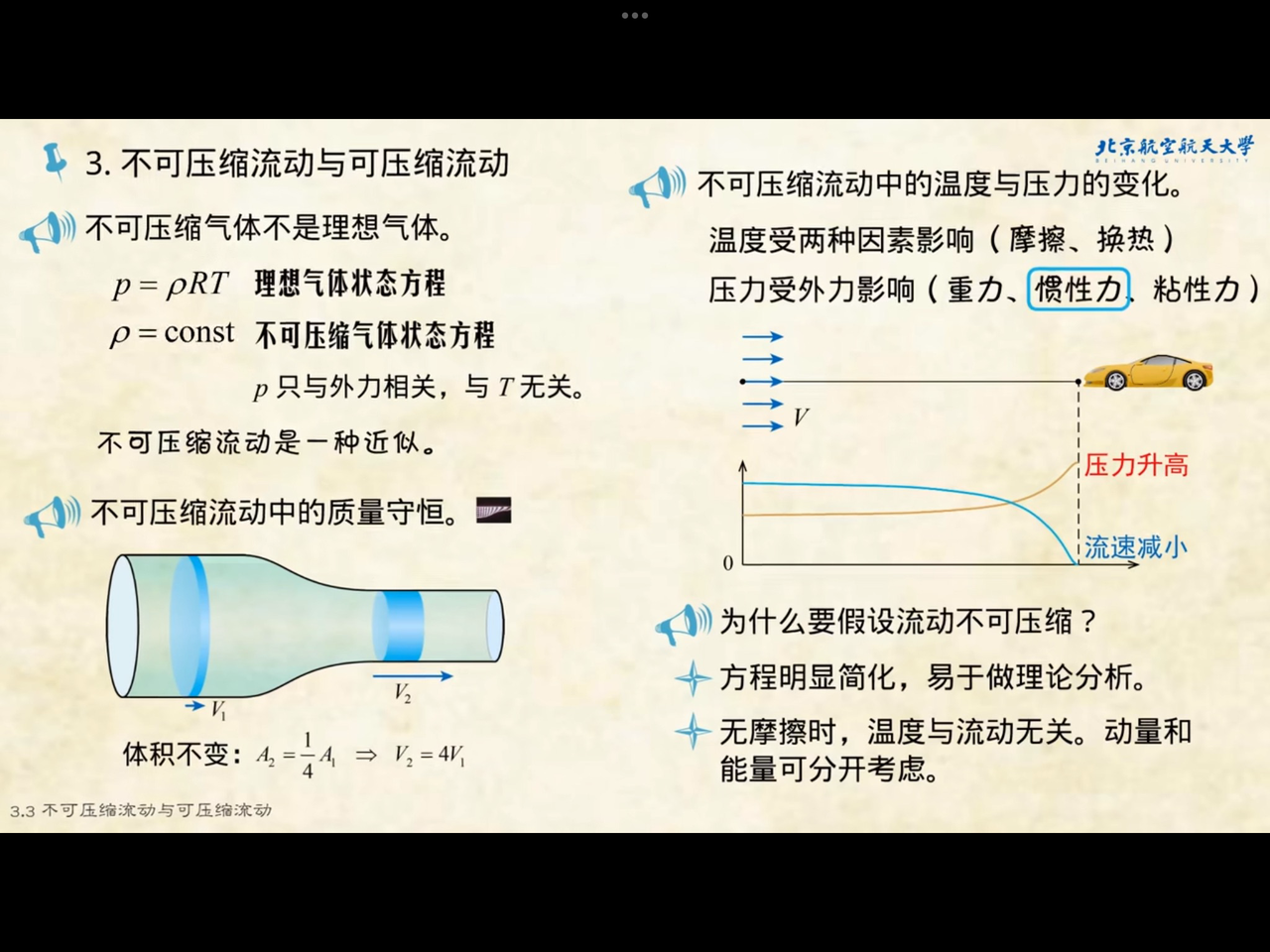
不可压缩的均质流体
如果流体的任何子区域的体积随时间恒定不变,则该流体是不可压缩的。如果流体的密度r在空间中恒定,则该流体是均质的。不可压缩性和均匀性的结合意味着密度在时间和空间上都是恒定的。这些假设在流体动力学中很常见,并且它们不会降低由此产生的数学对模拟真实流体(例如水和空气)的适用性。
拉格朗日法
拉格朗日法,侧重于对流体微元的描述,它去哪,我就一直研究它的性质。对于拉格朗日法而言,研究的是时间、质点和速度、加速度的关系。 在流体建模中,拉格朗日法对应着粒子方案,即建模流体微团为粒子,从而在粒子或则气体颗粒的空间行进过程中对其加以跟踪,这可以根据标准的粒子系统方案解决;该技术的优点在于,其处理过程类似于刚体动力学从而获得简化;该方案缺点是,当模拟高密度且分布较广的流体时,需要使用大量的粒子。
欧拉法
欧拉描述侧重于对空间的描述,将场划分为一个个极小的空间,并研究空间内的流体分布情况。对于欧拉法而言,研究是时间、位置和速度、加速度的关系。 在流体建模中,欧拉法对应着网格方案,即将空间分解为独立的网格单元,并对网格单元中的气体进行计算;通过该方式,各网格中的气体密度可在各时间步之间进行更新;在渲染过程中,各个网格内的密度值将确定气体的可见性以及图形形态。
Navier-Stokes equations
在数学上,流体在给定时刻的状态被建模为速度矢量场:为空间中的每个点指定速度矢量函数。 Navier-Stokes方程是速度场随时间演化的精确描述,给定当前速度矢量场和力场,方程就可以告诉我们矢量场是如何在dt上变化的。
等式 1
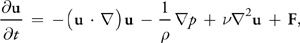
其中 \(\rho\) 是(恒定)流体密度,\(\nu\) 是运动粘度,\(F = (f_x, f_y)\) 表示作用在流体上的任何外力。

Navier-Stokes 方程是二阶非线性偏微分方程,不易求解,故有一系列简化情况,其中一种简化如下文所推演。
等式 2
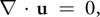
在假设流体是不可压缩的均质流体时,可得上式,进而简化方程。
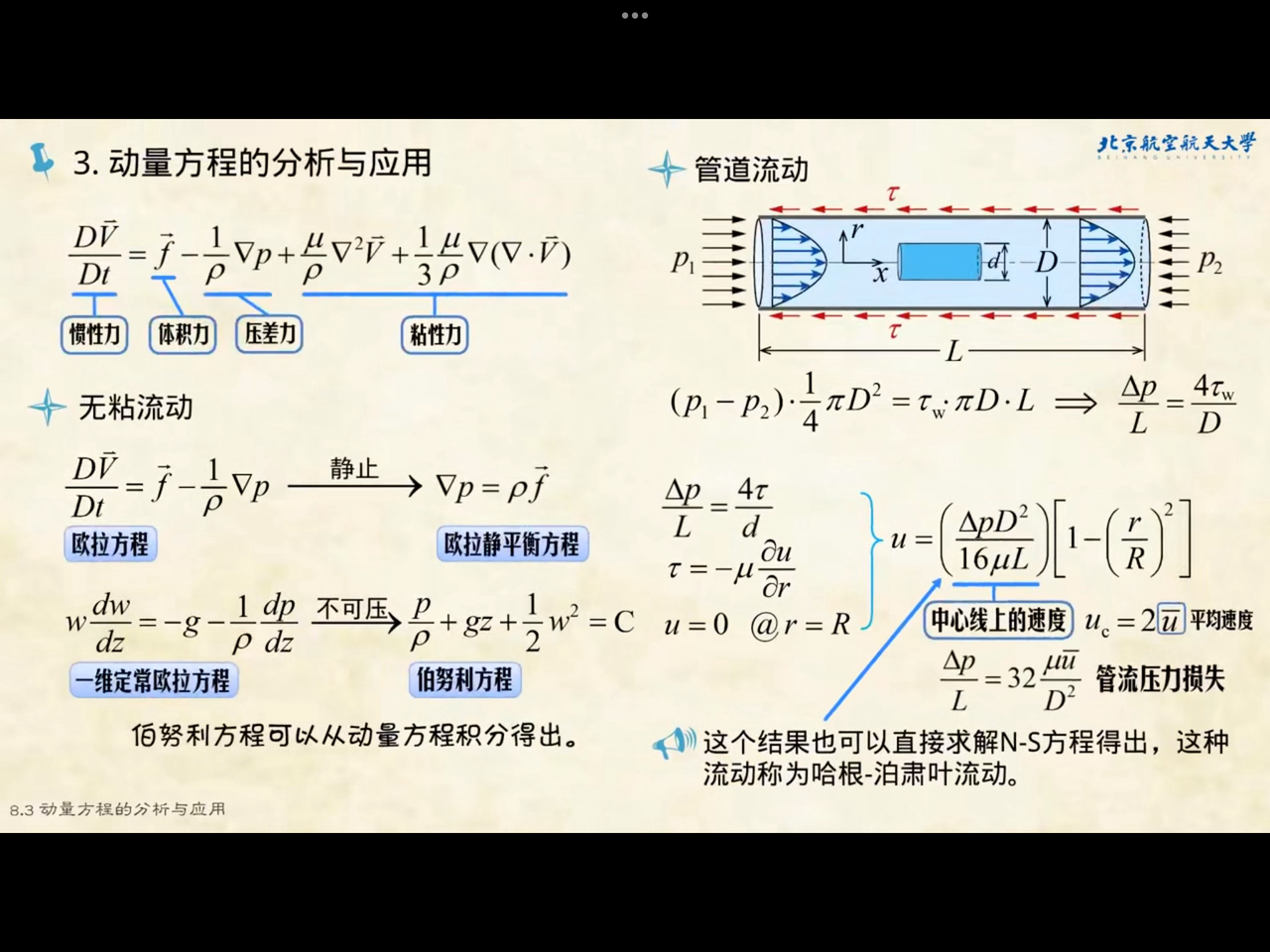
如何把向量场弄得跟理想流体一样不可压缩?换句话说,我们怎么将一个向量场变成无散场? 亥姆霍兹定理,或称向量分析基本定理解决了这个问题。
亥姆霍兹定理,或称向量分析基本定理,其指出: 对于任意足够光滑、快速衰减的三维向量场可分解为一个无旋向量场和一个螺线向量场的和,这个过程被称作亥姆霍兹分解。
这意味着任何矢量场 F,都可以视为两个势场(标势 φ 和矢势 A)之和。 在矢量分析中,一螺线矢量场(solenoidal vector field)是一种矢量场v,其散度为零,即无散场。
问题再次转化为【要减去什么标量场的梯度场】?答案是流体的压力场。而压力,我们都知道,压力是一种体积力,是传递到流体各处的,所以没有一个特定的方向,是标量。
等式 3
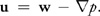
标量的梯度是无旋场这是散度和旋度的一个性质。 散度和旋度性质 散度和旋度有一些性质: 标量场的梯度为无旋场 矢量场的旋度为无源场 无旋场必可表为标量场的梯度 无源场必可表为另一矢量场的旋度
亥姆霍兹定理还引出了一种计算压力场的方法。如果我们将散度算子应用于
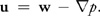
的两边,我们得到:
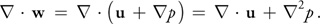
由于等式 2 ,这将简化为:
等式 4
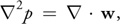
这是流体压力的泊松方程,有时称为泊松压力方程。
接着,类比于向量中的点积,我们可以使用亥姆霍兹-霍奇分解定理来定义一个投影算子,该投影算子的作用是将一个向量场w投影到它的无散度分量u上。 从而有:
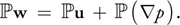
根据定义,一个无散矢量场的投影应当与自身相等,故:
\[\char"2119w = \char"2119u = u\]因此:
\[\char"2119{\nabla p} = 0\]将上述投影算子应用于原始 Navier-Stokes 方程,即等式1:
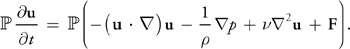
因为u是无散度的,所以左侧的导数也是无散度的:
\[\char"2119{\partial{u} \over \partial{t}} = {\partial{u} \over \partial{t}}\]此外,因为:
\[\char"2119{\nabla p} = 0\]所以可以舍去压力项,从而有:
等式 5
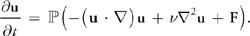
即简化流体运动为,对流、扩散、外力作用。 在流体建模实现中,我们会从左到右计算各个分量,每个分量都是一个步骤而不是一个因子,每个步骤取一个场作为输入,而用一个新的场做为输出。 对应数学表达为:
等式 6
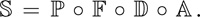
模拟算法的一个步骤可以表示为从右到左应用算子;首先是平流,然后是扩散、施力和投影。注意这里为了清晰起见省略了时间,但在实践中,每个算子的计算都必须使用时间步长。 从而可以归结出模拟过程伪代码为:
// Apply the first 3 operators in Equation 12.
u = advect(u);
u = diffuse(u);
u = addForces(u);// Now apply the projection operator to the result.
p = computePressure(u);
u = subtractPressureGradient(u, p);
其中,平流计算的式子在此直接给出,具体说明可以看下面流体算法步骤拆分:
等式 7
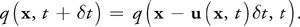
同时,扩散计算的式子也在此直接给出,具体说明可以看下面流体算法步骤拆分:
等式 8
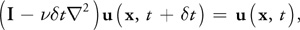
问题也就来到了求解两个泊松方程:泊松压力方程和粘性扩散方程。使用迭代求解技术,从近似解开始并在每次迭代中逼近真实解。 我们这里直接使用一个数学结论:如果网格单元是方形的,\(\nabla^2p\)(拉普拉斯算子)可以简化为:

从而等式 4 和等式 8 都可以离散化为:
等式 9
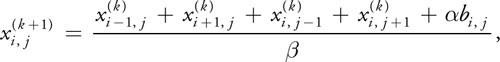
其中a和b是常数。两个方程的\(x\)、\(b\)、\(\alpha\)和\(\beta\)的值不同。 在泊松压力方程中,\(x = p\),\(b = \nabla . w\),\(\alpha = -(\delta x)^2\),\(\beta = 4\)。 对于粘性扩散方程,\(x = u\),\(b = u\),\(\alpha = (\delta x)^2 / v \delta t\),\(\beta = 4 + \alpha\)。
在完成上述两个方程求解后,我们开始处理外力作用。在 GPU Gems 以及常见的一些 2D 流体示例中,采用了直观的鼠标点击和拖动来对流体施加外力;更具体一点来说,在点击位点绘制外力施加点,并加以半径构建一个圆形范围,该圆内各点受外力随半径而衰减,这样一个斑点在 GPU Gems 中被称为“Splat”;其常见的构建表达如下:
等式 10
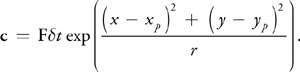
这里,F是根据鼠标拖动的方向和长度计算的力,r是外力施加半径,\((x, y)\)和\((x_p, y_p)\)分别是窗口中的片段位置和点击位置坐标。
流体算法步骤拆分
平流计算
Advection 平流的计算为,根据当前的流速,反推时间 deltaTime 后流到的网点位置。 下面阐述下为何没有按照常规的粒子系统的正推时间进行计算。 为了计算一个量的平流,我们必须更新每个网格点的数量。因为我们正在计算一个量如何沿速度场移动,所以想象每个网格单元由一个粒子表示会有所帮助。计算平流结果的第一次尝试可能是像更新粒子系统一样更新网格。只需将每个粒子的位置r沿着速度场向前移动它在\(\delta t\)时间中将行进的距离:
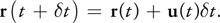
这是一种对常微分方程进行显式(或前向)积分的简单方法,即是常规的粒子系统的正推时间计算。 这种方法有两个问题:
- 第一个是使用显式对流方法的模拟对于大的时间步长是不稳定的。
- 第二个问题是特定于 GPU 实现的。我们在片段程序中实现我们的模拟,它不能改变他们正在编写的片段的位置。这种前向积分方法需要能够“移动”粒子,因此无法在当前的 GPU 上实现。 解决方案是反转问题并使用隐式方法(Stam 1999)。我们不是通过计算粒子在当前时间步长上移动的位置来计算平流量,而是将粒子从每个网格单元的轨迹及时追溯到其先前位置,并将该位置的数量复制到起始网格单元。要更新数量q(这可以是速度、密度、温度或流体携带的任何数量),我们使用以下等式:
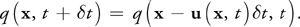
其反溯过程如下图所示:
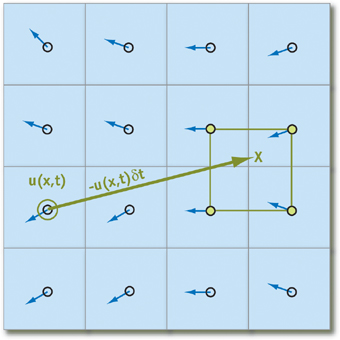
对于反溯获得的上一时的位点x而言,可以通过GPU的像素双线性插值获取。
以下代码是平流计算的示例:
void advect(float2 coords : WPOS, // grid coordinates
out float4 xNew : COLOR, // advected qty
uniform float timestep,
uniform float rdx, // 1 / grid scale
uniform samplerRECT u, // input velocity
uniform samplerRECT x) // qty to advect
{
// follow the velocity field "back in time"
float2 pos = coords - timestep * rdx * f2texRECT(u, coords);
// interpolate and write to the output fragment
xNew = f4texRECTbilerp(x, pos);
}
在这段代码中,参数u是速度场纹理,x是要平流的场。这可能是速度或其他数量,例如染料浓度。函数f4texRECTbilerp()是一个实用程序,用于对最接近传递给它的纹理坐标的四个纹素执行双线性插值。 代码实现与上面的算式有一点细微的不同。这是因为纹理坐标与我们的模拟对象场的单位不同(纹理坐标在 [0, N ]范围内,其中N是网格分辨率),我们必须将速度缩放到网格空间([0, 1])。这反映在 Cg 代码中,局部速度乘以参数rdx,该参数代表网格尺度x的倒数(对应于Unity ShaderLab中即乘以 name##_TexelSize)。纹理环绕模式必须设置为CLAMP_TO_EDGE,以便范围 [0, N ]之外的回溯将被限制到边界纹素。稍后描述的边界条件会正确更新这些纹素,以便这种情况正确运行。
扩散计算
粘性流体具有一定的流动阻力,这会导致速度扩散(或耗散)。粘性扩散的偏微分方程为:
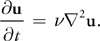
基于与平流计算类似的原因,我们采用隐式计算方式:
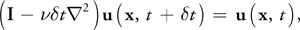
以下代码是扩散计算的示例:
void jacobi(half2 coords : WPOS, // grid coordinates
out half4 xNew : COLOR, // result
uniform half alpha,
uniform half rBeta, // reciprocal beta
uniform samplerRECT x, // x vector (Ax = b)
uniform samplerRECT b) // b vector (Ax = b)
{
// left, right, bottom, and top x samples
half4 xL = h4texRECT(x, coords - half2(1, 0));
half4 xR = h4texRECT(x, coords + half2(1, 0));
half4 xB = h4texRECT(x, coords - half2(0, 1));
half4 xT = h4texRECT(x, coords + half2(0, 1));
// b sample, from center
half4 bC = h4texRECT(b, coords);
// evaluate Jacobi iteration
xNew = (xL + xR + xB + xT + alpha * bC) * rBeta;
}
请注意,rBeta参数是等式 9 中的\(\beta\)倒数。为了求解扩散方程,我们将\(\alpha\)设置为\(\alpha = (\delta x)^2 / v \delta t\),rBeta 设置为\({1 \over \beta} = {1 \over {4 + \alpha}} = {1 \over {4 + (\delta x)^2 / v \delta t}}\),以及设置速度纹理的x和b参数。然后我们运行多次迭代(通常是 20 到 50 次,但可以使用更多迭代来减少错误)。
投影
上面我们提到,对于流体的场投影步骤分为两个操作:求解p的泊松压力方程,以及从中间速度场中减去p的梯度。 压力计算
void divergence(half2 coords : WPOS, // grid coordinates
out half4 div : COLOR, // divergence
uniform half halfrdx, // 0.5 / gridscale
uniform samplerRECT w) // vector field
{
half4 wL = h4texRECT(w, coords - half2(1, 0));
half4 wR = h4texRECT(w, coords + half2(1, 0));
half4 wB = h4texRECT(w, coords - half2(0, 1));
half4 wT = h4texRECT(w, coords + half2(0, 1));
div = halfrdx * ((wR.x - wL.x) + (wT.y - wB.y));
}
梯度相减
void gradient(half2 coords : WPOS, // grid coordinates
out half4 uNew : COLOR, // new velocity
uniform half halfrdx, // 0.5 / gridscale
uniform samplerRECT p, // pressure
uniform samplerRECT w) // velocity
{
half pL = h1texRECT(p, coords - half2(1, 0));
half pR = h1texRECT(p, coords + half2(1, 0));
half pB = h1texRECT(p, coords - half2(0, 1));
half pT = h1texRECT(p, coords + half2(0, 1));
uNew = h4texRECT(w, coords);
uNew.xy -= halfrdx * half2(pR - pL, pT - pB);
}
扩展
染料模拟
上面介绍了 2D 流体模拟的理论依据和算法过程,上述算法过程模拟的可以是流动的液体或则气体的速度变化,但对于染料而言,我们需要更多额外数据表达,以进行染料的颜色和扩散过程的模拟。 假设\(d\)是染料浓度,则染料场的演变由以下方程控制:
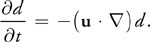
为了模拟流体如何携带染料,我们将平流算子应用于标量场,就像我们对速度所做的一样。如果我们还想考虑染料在流体中的扩散,我们添加一个扩散项:
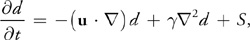
其中\(\gamma\)是染料在水中的扩散系数,为了实现染料扩散,我们使用 Jacobi 迭代,就像我们对速度的粘性扩散所做的一样;\(S\)则是染料源,这个可以通过类似于外力施加的方式进行建模。 涡旋
卷曲计算
Curl 卷曲计算为根据当前格子周围格子的速度,计算出当前网点的旋转速度。这个量是垂直于计算依赖平面的。 涡旋计算
参考
- https://zhuanlan.zhihu.com/p/263053689
- https://developer.download.nvidia.cn/books/HTML/gpugems/gpugems_ch38.html
- https://github.com/QianMo/GPU-Gems-Book-Source-Code/blob/master/GPU-Gems-1-CD-Content/Beyond_Triangles/Fluids/Flo/flo.cg
- https://wolfchen.top/ltmn/
- http://jamie-wong.com/2016/08/05/webgl-fluid-simulation/
- http://graphics.cs.cmu.edu/nsp/course/15-464/Fall09/papers/StamFluidforGames.pdf
- https://www.dgp.toronto.edu/public_user/stam/reality/Research/pdf/ns.pdf
- https://pdfs.semanticscholar.org/5127/ac7b58e36ffd13ca4437fc123c6a018dc436.pdf?_ga=2.205924112.2024347833.1637113470-1189970163.1637113470
- 《计算机动画——算法与技术》8.2计算流体动力学